22 Fondus de polymères

Il y a chaîne idéale confinée et chaîne idéale confinée ...

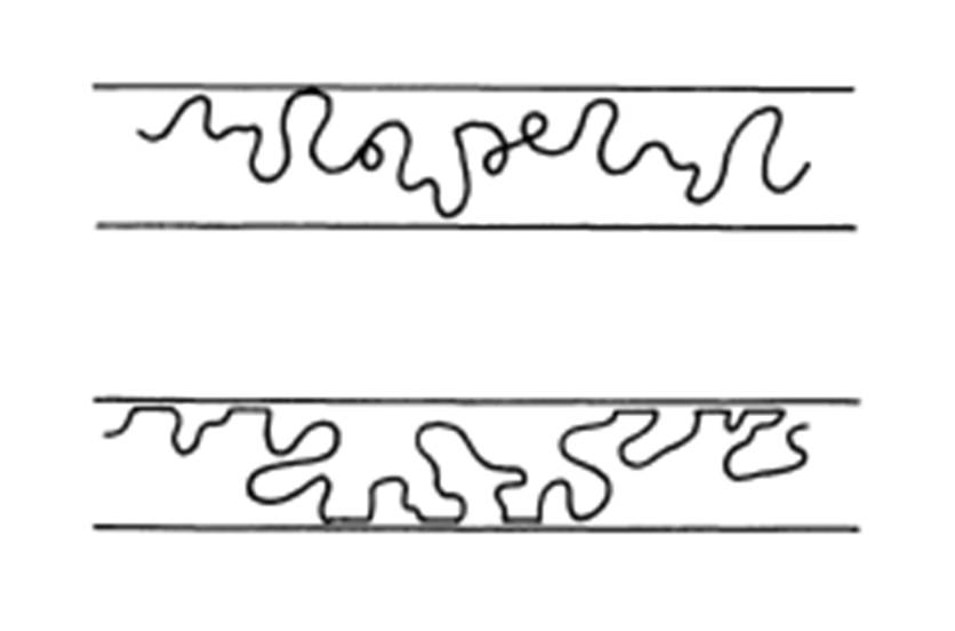La configuration d'une chaîne de polymère isolée dans un solvant theta et celle d'une chaîne d'un polymère fondu s'apparentent toutes deux à des marches au hasard. Pourtant, lorsque ces chaînes sont confinées entre deux murs neutres, leurs configurations deviennent très différentes. La concentration de polymère est inhomogène dans le premier cas, et homogène, y compris en surface, dans le second.

Je déteste le plastique mais je dois avouer que je suis fondu de problèmes de polymères. Mon premier contact avec ces systèmes s'est produit pendant une année passée  chez IBM à San Jose, dans le contexte d'un débat entre les théoriciens Chris Baker, adepte des méthodes de champ moyen, et Pierre-Gilles de Gennes, génial inventeur des lois d'échelle dans les polymères. Le débat concernait la force attendue à l'équilibre pour confiner un polymère fondu entre deux plaques (le lien avec IBM est la lubrification des têtes de lecture). Une force répulsive devait exister selon le premier, aucune selon le second. Après un travail expérimental peu convaincant avec la méthode SFA (Surface Force Apparatus), trop sujette aux artéfacts thermiques, je me suis penché sur ce problème avec des outils statistiques introduits dans les polymères par di Marzio pour décrire les édifices semi-cristallins (problème dit de la ruine du joueur) et via des simulations numériques avec G. Ten Brinke et G. Hadziioannou. Les deux approches sont arrivées à la même conclusion que de Gennes : pas de force pourvu que le polymère confiné puisse s'échanger avec un réservoir en volume. Ce travail utilise un truc qui simplifie beaucoup les calculs, et qui a été repris par O. Guiselin (1992), puis M. Aubouy (2000) pour l'étude de polymères adsorbés ou fondus. Il consiste à assimiler une boucle (aller-retour sur la surface) à deux queues (aller simple vers le volume), qui sont statistiquement équivalentes. Ce travail m'a permis de développer une image des polymères fondus qui est la suivante : pour un polymère infiniment flexible, aucune orientation des segments (liaisons chimiques) qui le constituent n'est nécessaire en dehors de la surface pour assurer une densité uniforme. Toute la contrainte du confinement est portée par l'orientation des segments en contact avec la surface, et l'énergie correspondante par unité de surface ne varie pas avec la distance entre les plaques. Ce schéma s'applique aussi aux solutions semi-diluées si on remplace les segments par des "blobs".

Il m'a permis très récemment de donner une image simple d'un effet  très connu : l'augmentation de la tension interfaciale d'un fondu avec la longueur des chaînes, dit "effet d'extrémités".

De façon un peu paradoxale, l'étude des fondus confinés (écrasés) facilite aussi la compréhension des fondus étirés et greffés (les "brosses") dont les copolymères diblocs sont un exemple très répandu. En effet, la littérature sur le sujet ignore, à ma connaissance totalement, qu'aucun étirement des chaînes n'est nécessaire dans la direction perpendiculaire à la surface tant que la densité de greffage reste suffisamment faible, à savoir une chaîne par surface Na^2/3, avec N la longueur de la chaîne et a la taille d'un segment. Comme le volume d'une chaîne est Na³, cela correspond à une épaisseur Na^1/3. C'est le seuil d'épaisseur pour l'apparition d'une énergie élastique. Cette remarque a des conséquences importantes sur l'épaisseur d'équilibre des couches de copolymères et sur leurs propriétés de mouillage. La référence de ce travail, effectué en hommage à Loïc Auvray, est Eur. Phys. J. E  (2018) 41: 74.